OctopusLAB 76
Von Neumannova architektura počítačů
Konečně se na své cestě historií výpočetní techniky dostáváme k elektronickým počítačům. V tomto díle zmíníme základní koncept, se kterým pak budeme dále pracovat.
Nebylo vždy zjevné, že i nejjednodušší počítací stroj (například kalkulačka) by měl mít nějaké vstupní rozhraní (třeba klávesnice čísel a matematických operací). Pak je tu část, která vstupní data zpracuje (v případě jednoduchého výpočtu nám stačí aritmetická jednotka) a výsledek chceme nějak zobrazit na výstupu (třeba displeji). Úplně první počítače (například Z1 nebo ENIAC) byly velmi komplexní zařízení, kde ještě nebylo zcela jasné, jak elegantně takový stroj „programovat“. Jak rozlišit a především jak ukládat uživatelská data (a že proměnné lze snadno oddělit od programu a přitom je mít uloženy podobně). Využívaly se dostupné prvky z telegrafie, telefonie. To je hezky vidět na prvních programovacích panelech, které měly podobný vzhled jako telefonní ústředny a postupně se začaly jako „přepínače“ více používat i elektromagnetická relé. A jedny z prvních vstupních a výstupních zařízení byly dálnopisy (ze kterých jsme si až do dneška zachovali některé specifické řídící znaky).
Některé z prvních počítacích strojů byly dokonce navrženy pro počítání v desítkové soustavě. Vidět tak můžeme sady tlačítek a žárovek (0,1 ,2, 3, … až 9), podobně jako na starých mechanických pokladnách. Výhody dvojkové soustavy se však prosadily poměrně rychle.
Nejstarší výpočetní stroje měly programy pevně zabudované v hardwaru a jejich změna často znamenala úplnou změnu hardwaru stroje. Název von Neumannova architektura se vžil na základě přednášky matematika Johna von Neumanna. Přednášku „First Draft of a Report on the EDVAC“ věnovanou právě návrhu počítacího stroje s uloženým programem přednesl v červnu roku 1945. Nicméně stejná koncepce se objevila v některých amerických patentech již od roku 1936. (Wikipedia)
Dnes už každý tuší, k čemu bylo nutno se na občas strastiplné pouti dopracovat a když vidíte následující nákres, neměl by vás už moc překvapit. Podobnou strukturu mají i dnešní počítače, dokonce i chytré mobilní telefony. Také náš oblíbený mikrokontrolér ESP32 sdílí stejnou architekturu.
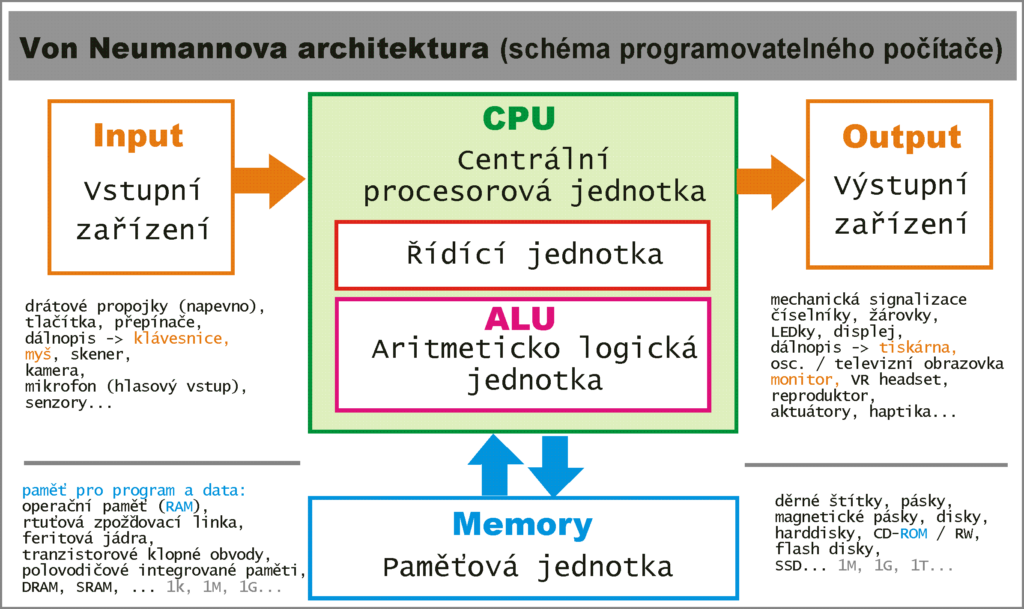
Dovolím si ještě připomenout další dva významné průkopníky, kteří byli pro vývoj prvních počítačů zásadním přínosem.
Alan Turing (kterého jsem v Hamíkovi už párkrát zmínil) už v roce 1936 představil koncept teoretického modelu obecného výpočetního stroje (Turingův stroj), který se stal jedním ze základů informatiky.
V následujícím roce 1937 německý inženýr Konrad Zuse předložil dva patenty předvídající von Neumannovu architekturu. Počítač se stručným názvem Z1 podle jeho návrhu byl dokončen v roce 1938. Obsahoval 30 tisíc kovových částí a nepracoval správně kvůli nedostatečné mechanické přesnosti. Po roce 1939 však dostal finanční prostředky od vlády nacistického Německa a jeho další stroje měly být využívány „pro válečné účely“.
V dalších dílech mám v plánu popisovat různé části počítačů, z nichž některé si i sestrojíme, oživíme a pokusíme se je propojovat do větších celků. Projekt Octopus_23_RUR (retro ultra replika) bude výuková experimentální sestava, která by mohla umět emulovat celou řadu opravdu historických počítačů (EDSAC, PDP) nebo prvních dostupných osmibitů (IMSAI8080, Altair8800, …). Některé části budeme pouze emulovat, ale základní principy se pokusíme zachovat.
Spojte se s námi na Twitteru, Facebooku nebo Instagramu, kam se snažíme pravidelně vkládat aktuální novinky.
OctopusLAB 77
Zobrazování čísel a číselné soustavy
Jelikož už i základ výrazu počítač tvoří slovo počítat, chvíli se ještě zdržíme u jednoduchých „počtů“.
Proč počítače používají takzvanou dvojkovou soustavu a co to znamená? Právě i to se vám pokusíme opět co nejstručněji přiblížit.
Pokusy sestrojit elektronické počítače tak, aby mohli pracovat s lidem srozumitelnou desítkovou soustavou totiž navazovaly na první mechanické počítací stroje (soustava ozubených koleček s přenosem desítky). Brzy se ukázalo, že není snadné spolehlivě rozlišit deset různých elektrických hodnot a především je dále zpracovat a uchovat. Takže se zvolila pro konstruktéry jednodušší možnost. Ta je založena na principu rozlišení pouze dvou hodnot: žárovka svítí / nesvítí, spínač je sepnut / rozepnut, signál má jednu nebo druhou (nulovou) hodnotu napětí. Ukázalo se, že to funguje dobře a proto se binární (dvojková) soustava bez větších problémů velmi rychle prosadila.
Ale vraťme se opět ještě trochu do vzdálené minulosti, kdy lidé ještě objevovali možnosti jak pracovat s teprve se rodícími čísly. Historie matematiky je velmi zajímavá, ale tentokrát to budou opravdu jen jednoduché počty. Jistě známe a používáme desítkovou soustavu, která vychází z toho, že lidé nejspíš začali počítat na prstech a prstů (na rukou) mají lidé deset.

Na obrázku vidíme deset očíslovaných prstů (od jedničky do desítky). Jen namátkou jsme vybrali i dvě archaická a trochu exotická zobrazení čísel. Mayská čísla – v trochu zvláštní dvacítkové soustavě, kde škeble znázorňovala násobek dvaceti a v jistých případech i jakousi nulu. Pro další větší čísla pak byly používány složité piktografické symboly.
Nám více známé římské číslice zase ukazují, že počítat s čísly takto napsanými bylo velmi obtížné (a některé operace s nimi takřka nemožné). Teoreticky by se mohlo jednat o nepoziční soustavu „sedmičkovou“, jelikož využívají sedm různých symbolů (I=1, V=5, X=10, L=50, C=100, D=500, M=1000), ale specifická pravidla pro zobrazování větších čísel jí přisuzuje kombinaci soustavy pětkové a desítkové.
Sumerové a Babyloňané (již zhruba před 4000 lety) používali poziční soustavu, ve které hodnotu zapsaného čísla určují pozice jednotlivých znaků. Základem jejich soustavy bylo číslo 60. Šedesátkovou soustavu používáme dodnes pro počítání času a při měření úhlů (60 se dobře dělí na polovinu, třetinu i čtvrtinu).
Pro dobré pochopení soustav využívaných při práci s počítači se zaměříme na poziční soustavy ve kterých počet použitelných symbolů odpovídá „číslu“ soustavy.
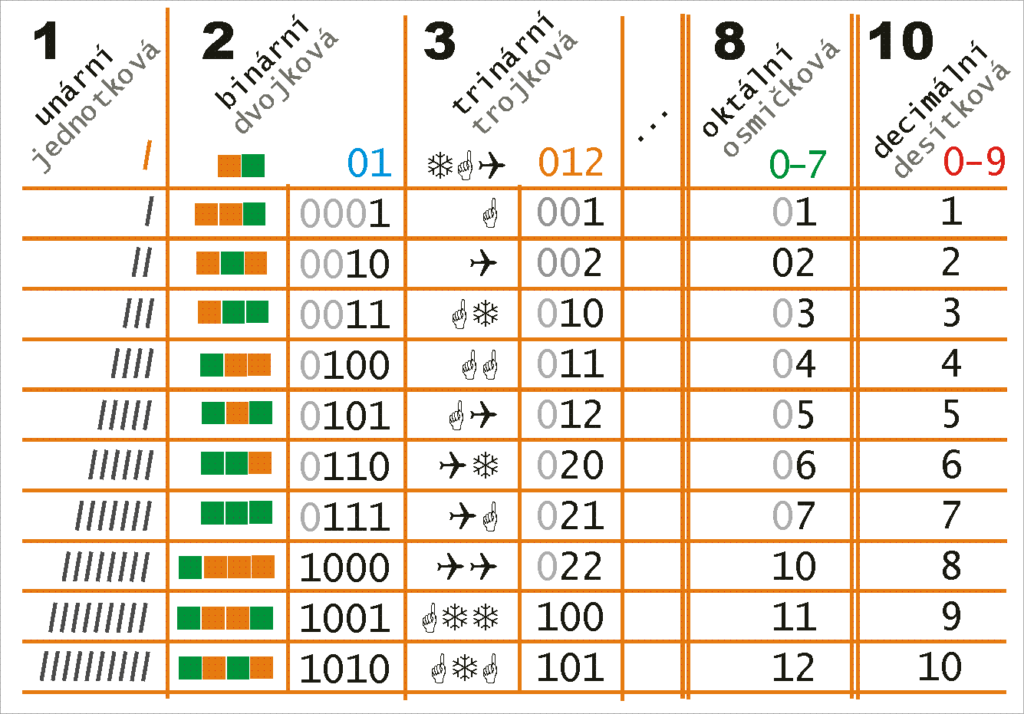
Na rozdíl od soustavy desítkové, kde máme k dispozici deset různých symbolů 0 1 2 až 9 a desítka už je s přenosem na další místo 10. V soustavě dvojkové máme tedy k mání pouze dva symboly: například nula a jedna, 0 / 1. U turingova stroje jsme používali dvě barvy: oranžovou a zelenou.
V soustavě trojkové bychom měli k dispozici symboly tři: 0 1 2 nebo na obrázku máme i variantu vločka, prst a letadlo (trinární nebo ternární soustava tří wingdings symbolů).
Aby nemuseli programátoři pracovat ve dvojkové soustavě, začala se používat i soustava osmičková (0 1 2 3 4 5 6 7) a šestnáctková. V šestnástkové (hexadecimální) soustavě a k symbolům 0 až 9 ještě přidalo ještě prvních šest písmen abecedy A B C D E F.
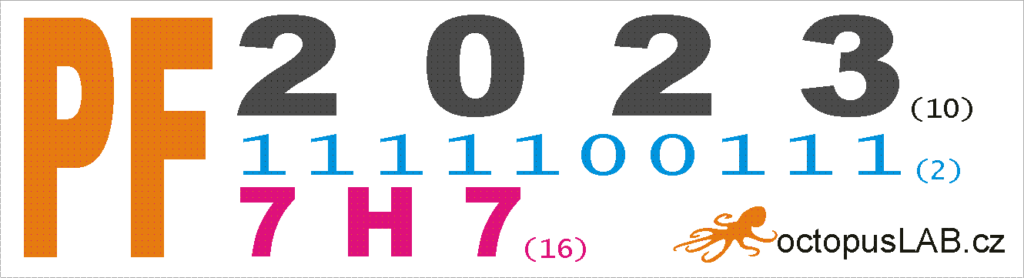
Všem čtenářům Hamíka si dovolím jménem Octopus LABu popřát vše nejlepší v novém roce 2023, hlavně zdraví a radost z tvoření.
Rok 2023 desítkově znamená dvě tisícovky, nula stovek, dvě desítky a tři jedničky.
Pozičně jednoduchý součet 2×1000 + 2×10 + 0x100 + 3×1 = 2023
Římskými číslicemi obdobně: MMXXIII.
Dvojkově (binárně) je to pak: 1111100111
1×1024 + 1×512 + 1×256 + 1×128 +1×64 + 0x32 + 0x16 + 0x8 + 1×4 +1×2 + 1×1 = 2023
V šestnáctkové soustavě (hexdecimálně) je to krásný palindrom 7E7.
(E = 14) pak 7×256 + 14×16 + 7×1 = 2023
OctopusLAB 78
Číselné soustavy využívané počítačem
Navážeme na minulý díl, kde jsme popřáli do nového roku v různých číselných soustavách. Povšimněte si, že když máme k dispozici pouze dva znaky, je číslo 2023 mnohem delší než když máme k dispozici znaků šestnáct (1111100111 oproti 7E7).

„Operátoři“ historických počítačů museli znát systém až na detailní technické úrovni a úplně první kódování se provádělo v binární (dvojkové) soustavě. Zadávat dlouhé řetězce nul a jedniček by vedlo k častým chybám a tak právě první zjednodušení bylo sdružování delších řetězců jedniček a nul do skupin.
V tabulce je ukázáno, jak zpřehledníme dvojkovou soustavu řazením do skupin. Červeně je značená oktalová (osmičková) soustava, která končí znakem ‚7‘, sdružuje binární číslice do trojic, zatímco dnes běžnější hexadecimální soustava (označená zeleně) zobrazuje nuly a jedničky ve skupinách po čtyřech.
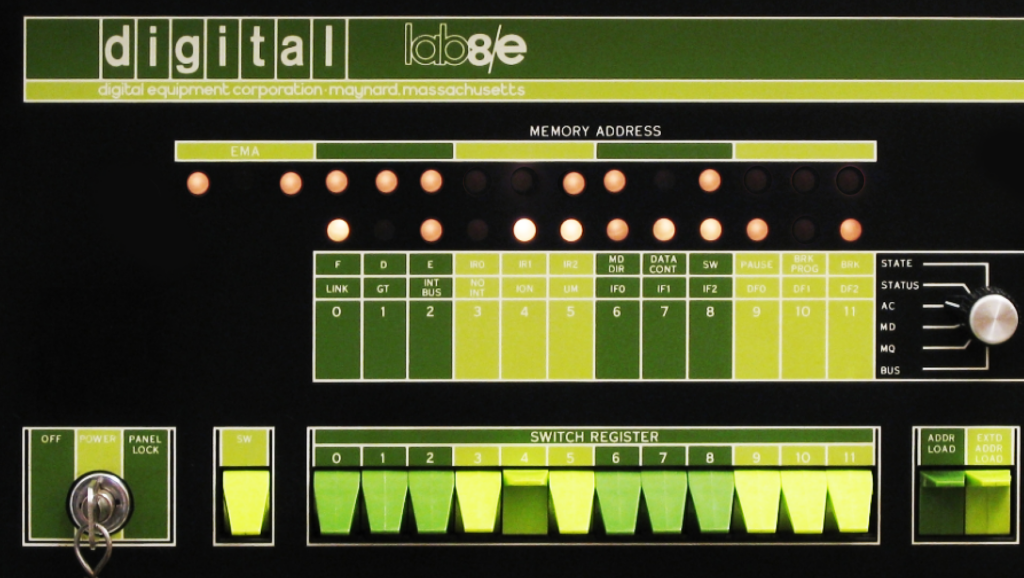
Počítač PDP8 byl uveden na trh někdy kolem roku 1965. Na obrázku je jedna z verzí lab8/e, kde je vidět sdružování po třech (světlejší a tmavší skupiny přepínačů). V horní části MEMORY ADDRESS pak je řada žároviček (to se ještě LEDky nepoužívaly), která zobrazuje dvojkové číslo 101 111 001 101 000.
Další verze už přešly na sdružování po čtyřech (s hexadecimální soustavou) a také na „logičtější řazení“ nižších bitů. Zde je ještě verze s nejnišším bitem vlevo „0123456789…“ (to bychom psali PF 3202 a ne 2023) ale pro nás je dnes už srozumitelnější a běžné mít nejnižší bit vpravo – „…9876543210“.
Pro zajímavost – podobný princip „zjednodušení“ je zaveden i v privátním klíči bitcoinu. Při délce 256 bitů se používá několik skupin po jedenácti bitech (s kontrolním součtem na konci), které určují 2048 možných kombinací pro každou skupinu. Jako „symbol“ je pak navrženo 2048 unikátních anglický slov, což nám tvoří specifickou „dvoutisícčtyřicetiosmičkovou“ soustavu.

——————————Pokud bude volné místo——————————
Možná je vhodné si připomenout jeden fakt z obecných mocnin a to že „libovolné číslo na nultou je jedna“. V číselných soustavách pak řešíme jednotky, desítky, stovky, tisíce… pro soustavu desítkovou.
Obdobně jedničky, dvojky, čtyřky, osmičky, šestnáctky… pro dvojkovou soustavu.

